13天 笔记整理 最后冲刺

最后这几天都是自己复习，干脆整理笔记自用

加油

高考会赢的

📚本文目录

---

🧪高中化学

反应类型 & 常见官能团 + 实例🌟🌟🌟🌟

反应类型	能发生的常见官能团	反应条件 或 特点	例子	化学方程式
消去反应	醇（-OH）卤代烃（-X）	醇：浓硫酸、加热（脱水）卤代烃：NaOH/醇溶液、加热（脱去HX）	乙醇在浓硫酸170°C下生成乙烯	C₂H₅OH → CH₂=CH₂ + H₂O（加热，浓H₂SO₄）
加成反应	烯烃（C=C）、炔烃（C≡C）醛（-CHO）、酮（-CO-）	常发生在不饱和键上；加 H₂、Br₂、HCl、H₂O 等	乙烯与溴加成生成1,2-二溴乙烷	CH₂=CH₂ + Br₂ → CH₂BrCH₂Br
取代反应	烷烃、苯及其衍生物（-Ph）醇（-OH）羧酸（-COOH）酯（-COO-）	烷烃：光照下卤素取代芳香烃：催化剂、卤化剂、硝化等	甲烷在光照下与氯气反应生成氯甲烷	CH₄ + Cl₂ → CH₃Cl + HCl（光照）
氧化反应	醇（-OH）、烯烃（C=C）醛（-CHO）、芳香烃	醇 → 醛/酮/羧酸 需强氧化剂如KMnO₄/H⁺、K₂Cr₂O₇/H⁺	乙醇被酸性高锰酸钾氧化为乙酸	CH₃CH₂OH + [O] → CH₃COOH + H₂O
还原反应	醛（-CHO）、酮（-CO-）硝基苯、酰胺、腈等	还原剂如LiAlH₄、NaBH₄；催化剂还原如H₂/Ni	乙醛被还原为乙醇	CH₃CHO + H₂ → CH₃CH₂OH（催化剂Ni、加热）
水解反应	卤代烃（-X）酯（-COO-、RCOOR’）酰胺（-CONH₂）、腈（-CN）	碱性或酸性催化，加热	溴乙烷的水解生成乙醇	C₂H₅Br + H₂O（碱性）→ C₂H₅OH + HBr
酯化反应	醇（-OH）与羧酸（-COOH）	浓硫酸，加热；可逆反应	乙醇与乙酸反应生成乙酸乙酯	CH₃CH₂OH + CH₃COOH ⇌ CH₃COOCH₂CH₃ + H₂O（浓H₂SO₄）
水解/皂化	酯（-COO-）：特别处理 – 油脂	NaOH溶液、加热	向酯中加入NaOH生成羧酸盐和醇	CH₃COOCH₂CH₃ + NaOH → CH₃COONa + CH₃CH₂OH
显色反应	酚（-Ph-OH） 淀粉（糖类）蛋白质（-CONH-）	与FeCl₃作用显紫蓝色（苯酚）遇碘显蓝（淀粉）遇浓硝酸显黄（蛋白质）	苯酚与三氯化铁反应显紫蓝色	C₆H₅OH + FeCl₃ → 紫蓝色络合物
卤化反应	烷烃、苯、醇	光照（烷烃），催化剂（苯），HBr等（醇）	光照下甲烷与氯气反应生成氯甲烷	CH₄ + Cl₂ → CH₃Cl + HCl（光照）
硝化反应	苯及其衍生物	浓硝酸 + 浓硫酸，加热	苯硝化生成硝基苯	C₆H₆ + HNO₃ → C₆H₅NO₂ + H₂O（浓H₂SO₄，加热）
加聚反应	烯烃（C=C）、某些炔烃（C≡C）	引发剂、加压、加热	乙烯加聚成聚乙烯	nCH₂=CH₂ → ­[–CH₂–CH₂–]n
缩聚反应	二元羧酸与二元醇/二元胺	催化剂、高温、逐步反应	对苯二甲酸与乙二醇缩聚成PET	HOOC–Ph–COOH + HOCH₂CH₂OH → [–OC–Ph–COOCH₂CH₂O–]n + (2n–1) H₂O

有机化学中常见官能团与 Na、NaOH、NaHCO₃、Na₂CO₃ 的反应总结🌟

官能团类别	与 Na 反应	与NaOH溶液反应	与NaHCO₃反应	与Na₂CO₃反应	主要产物	反应重要说明/规律
烷烃（-CH₃, -CH₂-）	❌ 否	❌ 否	❌ 否	❌ 否	无	通常不显酸性，任何试剂都无明显反应
烯烃（C=C）	❌ 否	❌ 否	❌ 否	❌ 否	无	性质稳定，不因弱酸碱与金属及盐反应
炔烃（C≡C）	❌ 否	❌ 否	❌ 否	❌ 否	无	通常不反应，某些末端炔如HC≡CH可与NaNH₂反应，但不考这类。
卤代烃（-X）	❌ 否	✅ 是	❌ 否	❌ 否	醇 / 酚	水解或亲核取代（如NaOH + CH₃CH₂Cl → CH₃CH₂OH + NaCl）
醇（R–OH）	✅ 是	❌ 否	❌ 否	❌ 否	醇钠、H₂ ↑	R–OH + Na → R–ONa + ½H₂↑酸性弱，仅与Na反应
酚（Ar–OH）	✅ 是	✅ 是	❌ 否	✅ 是	酚钠（Ar-ONa）NaHCO₃（只与Na₂CO₃）	酚酸性比醇强，而弱于碳酸，故不与NaHCO₃反应，但可以与NaOH、Na₂CO₃反应
羧酸（R–COOH）	✅ 是	✅ 是	✅ 是	✅ 是	羧酸钠、CO₂ ↑、H₂O、H₂ ↑	酸性强，反应均明显：R–COOH + NaHCO₃ → R–COONa + CO₂ ↑
酯（R–COOR’）	❌ 否	✅（可水解）	❌ 否	❌ 否	羧酸盐、醇	条件：NaOH加热 R–COOR' + NaOH → R–COONa + R’–OH
醛（R–CHO）	❌ 否	❌ 否	❌ 否	❌ 否	无反应	仅有锡/酸某些反应涉及，但一般不与Na、NaOH、碳酸盐直接反应
酮（R–CO–R’）	❌ 否	❌ 否	❌ 否	❌ 否	无反应	不显酸性，隐藏官能团需深入反应才能辨别
氨基（-NH₂）	❌ 否	（可参与水解）	❌ 否	❌ 否	季铵系，碱性弱反作用	若是酰胺，遇强碱可部分缓慢反应 (如苯甲酰胺 + 4NaOH → ...等)
硝基苯类(-NO₂)	❌ 否	❌ 否	❌ 否	❌ 否	无反应	有一定的酸性但用其他试剂作用；弱反应

选择题：含氧烃的衍生物

---

酸性的本质

酸的定义：在水溶液中电离出的阳离子全部为氢离子（H⁺）的化合物 ，其本质特征是能够向溶液中提供H⁺。

显而易见，如果溶液越容易放出H⁺，则溶液的酸性越强。总结高中阶段所学的知识，可以总结出以下因素：

1. 溶液电离程度

溶液越容易电离，电离程度越大，酸性越大

此外：

• 强酸 （如HCl、H₂SO₄、HNO₃）在水中完全电离 ，酸性强弱仅由浓度决定；
• 弱酸 （如CH₃COOH、H₂CO₃）在水中部分电离 ，酸性强弱由电离常数（Ka）决定；
• 酸性比较 需在相同条件 （同溶剂、同温度）下进行；

讲到溶剂，溶剂也是决定电离的一大因素

• 盐酸（HCl）在水中完全电离（强酸），但在冰醋酸中电离度显著降低；
• 醋酸（CH₃COOH）在水中为弱酸，但在液氨中可完全电离；

2. 键的极性&中心原子性质

吸电子原子A-H键极性越强，酸性越强

中心原子吸电子能力越强，酸性越强

这些理论适用于有机酸 （如羧酸、酚类）和无机含氧酸 （如硫酸、硝酸）

---

元素周期律

项目	内容	变化规律/应用	示例/说明
原子结构	原子序数=核电荷数=质子数=核外电子数（原子中）	电子层数=周期序数；最外层电子数=主族序数	H（1）、Li（2,1）、Na（2,8,1）
周期性本质	元素性质随原子序数递增呈现周期性变化	核外电子排布的周期性变化	同周期从左到右金属性减弱，非金属性增强
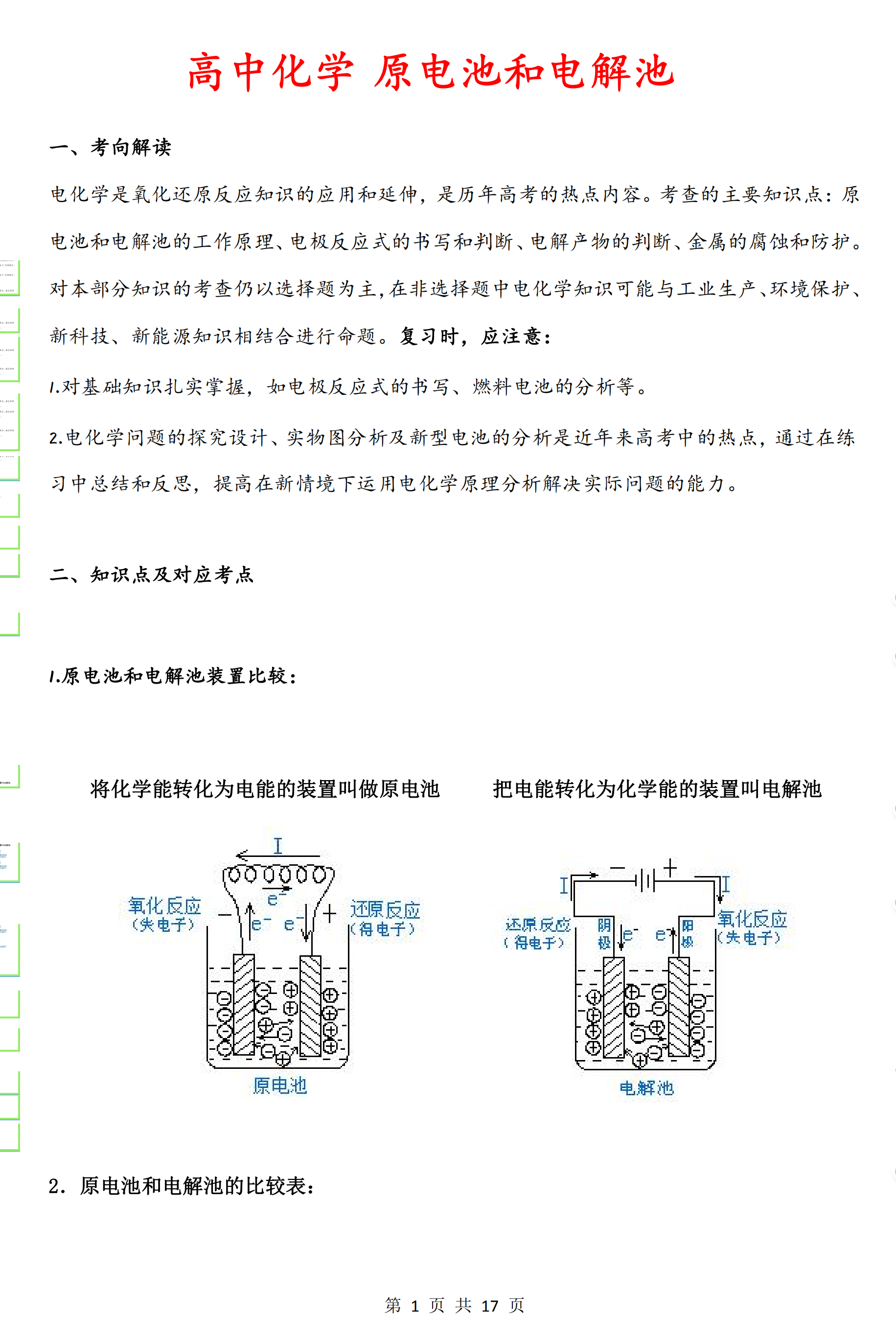
金属性比较	单质置换能力、与水/酸反应剧烈程度、最高价氧化物水化物碱性强弱	同周期左→右减弱；同主族上→下增强	Na>Mg>Al；LiCl>Br；N>O>F
原子半径	电子层数越多半径越大；同周期核电荷越大半径越小	同周期左→右减小；同主族上→下增大	Cl原子；阳离子<原子；同主族离子半径随原子序数增大
化合价	最高正价=族序数（O、F例外）；最低负价=主族序数-8	主族元素常见化合价规律	Cl最高+7（HClO₄），最低-1（HCl）
最高价氧化物酸碱性	酸性：非金属氧化物对应含氧酸；碱性：金属氧化物对应氢氧化物	酸性同周期增强，同主族减弱；碱性反之	HClO₄>H₂SO₄>H₃PO₄；NaOHHCl>HBr>HI

简单画成图：

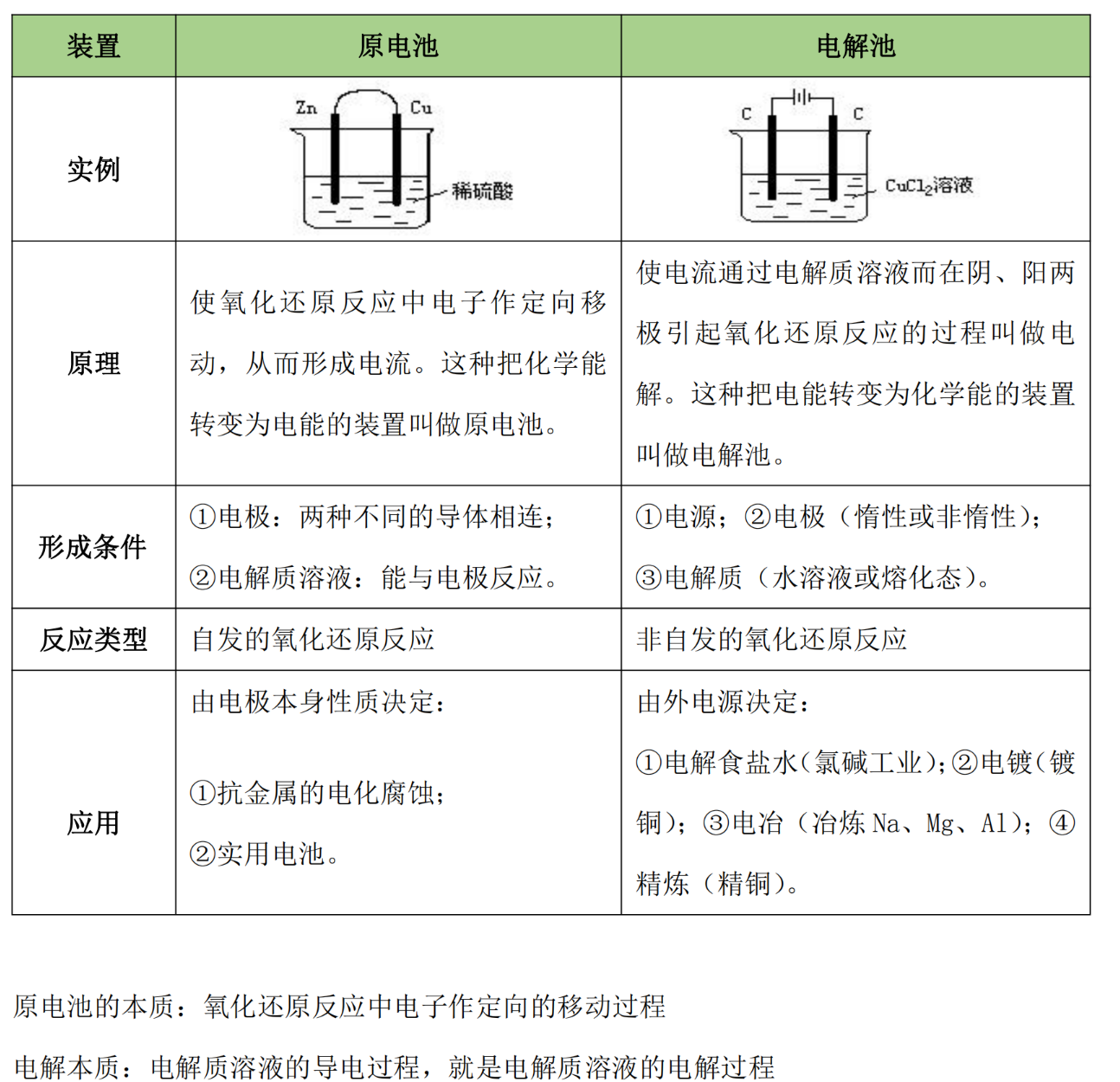
原电池 电解池

🔎高中物理

🏃‍♀️运动学

平抛运动常考内容

基础 重中之重！

平抛运动是匀变速运动，一般分解为水平的匀速运动和垂直的自由落体运动

推论可以不记，考试的时候可以把上面的公式联立得到推论。

动能 能量及其守恒

主要体型：

• 机车启动
  

🔍光学

⚡光的传播

公式	说明
c = 3×10⁸ m/s	真空中的光速，常用于各种波光换算
n = c / v	折射率定义式，n为介质折射率，v为介质光速
斯涅尔定律：n₁sinθ₁ = n₂sinθ₂	折射问题核心公式

🔍全反射相关🌟🌟

公式	说明
临界角：sin C = 1 / n	当入射角 ≥ C 时，发生全反射
条件：光从光密介质 进入 光疏介质	如：从玻璃进入空气、从水进入空气

🌊波动光学（干涉与衍射）🌟

现象	公式	说明
双缝干涉亮条纹	Δx = nλ	路程差为波长整数倍时为亮条纹
双缝干涉暗条纹	Δx = (2n + 1)λ/2	半波长奇数倍时为暗条纹
条纹间距公式	Δx = Lλ / d	L：双缝到光屏距离，d：双缝间距，λ：光波长

🔍透镜公式

公式	说明	备注
透镜成像公式：1/f = 1/u + 1/v	f：焦距，u：物距，v：像距	v为负数表示虚像，f为负表示凹透镜 (发散)

各类光特点总结🌟🌟

光的类型	折射率	光速	临界角
红光	最小	在介质中最快	最大，易接近不发生反射情况
紫光	最大	在介质中光速最慢	最小，易发生全反射

🔥热力学

常考与选择题基础，大题第一题

计算大题中常用公式🌟

• 理想气体的状态

• 摄氏度与开尔文转换

• 压强公式
  P=\frac{F}{S}

⚡电学

电场中的物理量的关系图

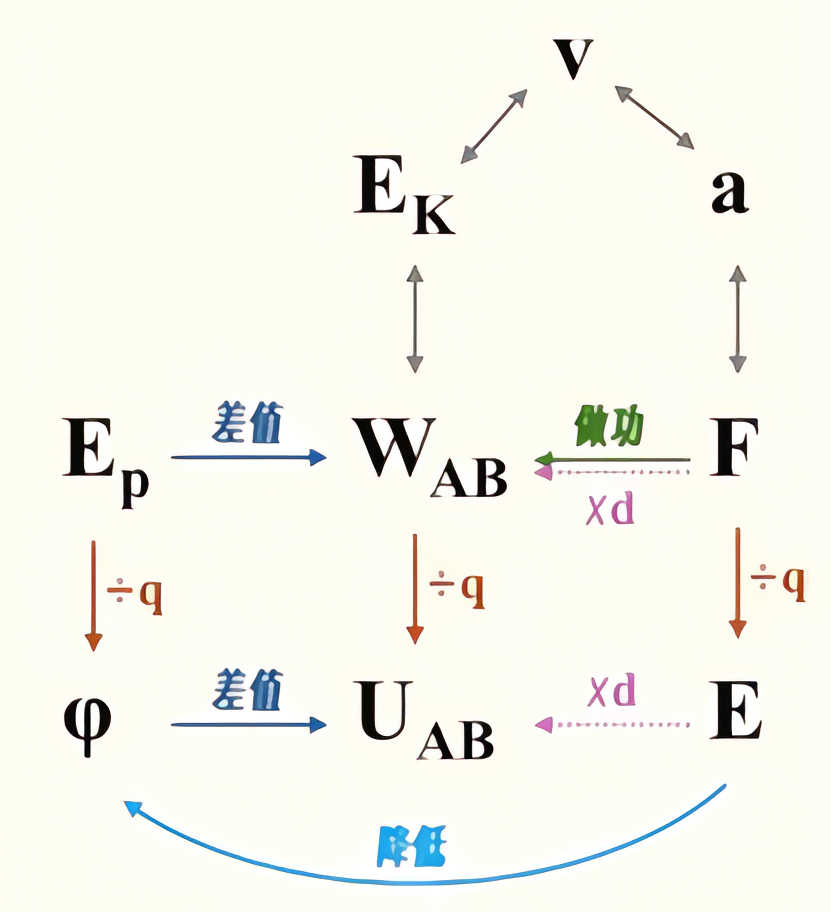
理想变压器和长距离输电

理想变压器：（只对正弦交流起作用）

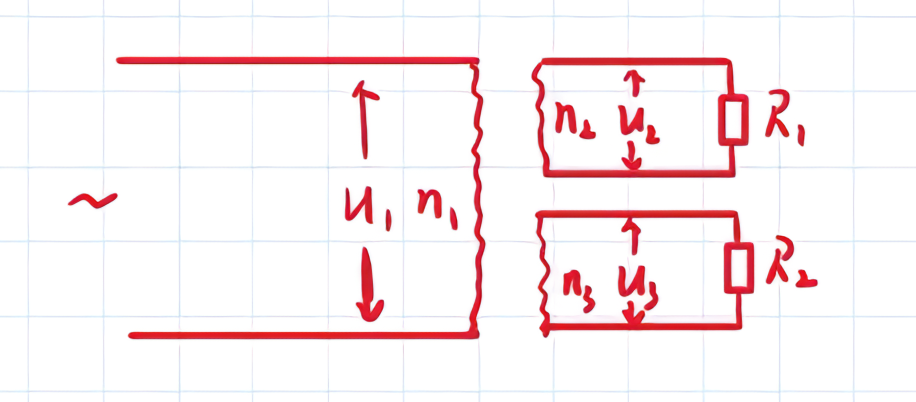
1. 电压关系：原线圈电压决定副线圈电压

   U_1 : U_2 = n_1 : n_2 \quad (\text{原理是电磁感应})

2. 功率关系：副线圈功率等于原线圈功率

   P_{\text{输入}} = P_{\text{输出}} \Rightarrow P_1 = P_2 + P_3 \quad (\text{原理是能量守恒})

3. 电流关系：

   P_1 = P_2 + P_3 \Rightarrow U_1 I_1 = U_2 I_2 + U_3 I_3

   单个副线圈：电流与匝数成反比

   P_1 = P_2 \Rightarrow U_1 I_1 = U_2 I_2 \Rightarrow \frac{I_1}{I_2} = \frac{U_2}{U_1} = \frac{n_2}{n_1}

远距离输电：高压输电减少电压和功率损耗

1. 电压关系：

   \frac{U_1}{U_2} = \frac{n_1}{n_2}, \quad U_2 = U_3 + 2I_2 r, \quad \frac{U_3}{U_4} = \frac{n_3}{n_4} \quad (\text{电压从左边来})

2. 功率关系：

   P_1 = P_2, \quad P_2 = P_3 + 2I_2^2 r, \quad P_3 = P_4 \quad (\text{功率从左边来})

3. 损耗电压和功率：

   \Delta U = 2I_2 r, \quad \Delta P = 2I_2^2 r

4. 发电机电动势：

   \mathcal{E}_m = nBS\omega, \quad \text{有效值 } U_m \text{ 不变}

5. 动态变化：
   用户多用电 \rightarrow P_4 \uparrow \rightarrow P_3 \uparrow, P_2 \uparrow \rightarrow I_1, I_2 \uparrow \rightarrow U_2 = U_3 + 2I_2 r \uparrow \rightarrow U_3 \downarrow \rightarrow I_4 \downarrow

🧲磁场 电生磁 磁生电

常用公式

类别	公式
磁感应强度定义式	B = \frac{F}{IL\sin\theta}
洛伦兹力	F = qvB\sin\theta
圆周半径	r = \frac{mv}{qB}
周期	T = \frac{2\pi m}{qB}
安培力	F = BIL\sin\theta
磁通量	\Phi = BS\cos\theta

这部分我是真没咋学，考试前多看n遍这个视频吧

📐高中数学

🔢数列复习

等差数列

1. 定义相邻两项的差为常数 d （公差）。

2. 通项公式

   a_n = a_1 + (n-1)d

   其中 a_1 为首项， d 为公差。

3. 前 n 项和公式

   S_n = \frac{n}{2}(a_1 + a_n) \newline \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = na_1 + \frac{n(n-1)d}{2}

4. 等差中项若三数 a, A, b 成等差数列，则等差中项为：

   A = \frac{a + b}{2}

5. 性质

   • 任意两项满足 a_n - a_m = (n - m)d （ n > m ）。
   • 若 m + n = p + q ，则 a_m + a_n = a_p + a_q 。
   • 单调性：当 d > 0 时，数列递增；当 d < 0 时，递减；当 d = 0 时，常数列。

等比数列

1. 定义相邻两项的比为常数 q （公比， q \neq 0 ）。

2. 通项公式

   a_n = a_1 \cdot q^{n-1}

   其中 a_1 为首项， q 为公比。

3. 前 n 项和公式

   • 当 q \neq 1 时：
     S_n = a_1 \cdot \frac{1 - q^n}{1 - q} \\ \ \ \ \ \ \ = a_1 \cdot \frac{q^n - 1}{q - 1}
   • 当 q = 1 时：
     S_n = n \cdot a_1

🧱立体几何体积面积公式🌟🌟🌟🌟🌟

几何体	表面积公式	体积公式	说明
台体（如圆台、棱台）	侧面积公式： S_{\text{侧}} = \frac{(C_1 + C_2)}{2} \cdot l 总表面积： S = S_{\text{上}} + S_{\text{下}} + S_{\text{侧}}	体积公式： V = \frac{1}{3} h (S_{\text{上}} + S_{\text{下}} + \sqrt{S_{\text{上}} S_{\text{下}}})	- C_1, C_2 ：上下底面周长- l ：母线长（斜高）- S_{\text{上}}, S_{\text{下}} ：上下底面积- h ：高
球体	表面积： S = 4\pi R^2	体积： V = \frac{4}{3} \pi R^3	- R ：球半径
锥体（如圆锥、棱锥）	侧面积公式： S_{\text{侧}} = \frac{1}{2} C \cdot l （圆锥： S_{\text{侧}} = \pi r l ）总表面积： S = S_{\text{底}} + S_{\text{侧}}	体积： V = \frac{1}{3} S_{\text{底}} \cdot h	- C ：底面周长- l ：母线长（圆锥的斜高）- S_{\text{底}} ：底面积- h ：高

---

🪙二项分布与超几何分布高考考点及解题总结

核心考点

1. 二项分布🌟🌟🌟

   • 定义：独立重复试验中，每次成功概率为 p ，重复 n 次，随机变量 X \sim B(n, p) 。
   • 典型场景：抛硬币、射击命中、独立事件重复发生。
   • 高频考法：
     • 求分布列或特定概率值（如 P(X=k) ）；
     • 计算期望 E(X) = np 和方差 D(X) = np(1-p) ；
     • 结合实际问题建模（如疫苗有效率、产品质量检测）。

2. 超几何分布🌟

   • 定义：从含 M 个次品的 N 个物品中不放回抽取 n 个，随机变量 X \sim H(N, n, M) 。
   • 典型场景：抽样检测、抽奖问题、有限总体的不放回抽样。
   • 高频考法：
     • 求分布列 P(X=k) = \frac{C(M,k) \cdot C(N-M, n-k)}{C(N,n)} ；
     • 判断模型适用性（如“无放回”关键词）；
     • 与二项分布对比分析（样本容量较小时差异显著）。

解题方法与公式

1. 二项分布公式

   P(X=k) = C(n,k) \cdot p^k \cdot (1-p)^{n-k}
   • 期望： E(X) = np
   • 方差： D(X) = np(1-p) 。

2. 超几何分布公式

   P(X=k) = \frac{C(M,k) \cdot C(N-M, n-k)}{C(N,n)}
   • 期望： E(X) = n \cdot \frac{M}{N}
   • 方差： D(X) = n \cdot \frac{M}{N} \cdot \frac{N-M}{N} \cdot \frac{N-n}{N-1} （常简化为近似公式）。

3. 关键解题步骤

   • 判断分布类型：
     • “独立重复”“成功率固定” → 二项分布；
     • “无放回抽样”“有限总体” → 超几何分布。
   • 列分布列：
     • 二项分布直接套用公式；
     • 超几何分布需枚举所有可能的 k 值并计算概率。
   • 期望与方差：直接代入公式，无需推导。

典型例题参考

1. 二项分布：
   • 抛一枚硬币5次，求恰好3次正面的概率（答案： C(5,3) \cdot 0.5^5 ）。
2. 超几何分布：
   • 盒中有10个球（3红7白），无放回取4个，求恰好2红球的概率（答案： \frac{C(3,2) \cdot C(7,2)}{C(10,4)} ）。

公式对比表

分布类型	应用场景	是否独立	期望公式	方差公式
二项分布	独立重复试验	是	np	np(1-p)
超几何分布	无放回抽样	否	n \cdot \frac{M}{N}	n \cdot \frac{M}{N} \cdot \frac{N-M}{N} \cdot \frac{N-n}{N-1}

📐三角函数

多练!!

没有技巧，全是感情和泪

解析几何

曲线类型	标准方程	参数定义	关系式	说明
椭圆	\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 （当 a > b 时）	- a ：长半轴长度 - b ：短半轴长度 - c ：焦点到中心的距离	c^2 = a^2 - b^2	焦点在长轴上（x轴方向） 若焦点在 y 轴，则 a > b 且标准形式为 \frac{y^2}{a^2} + \frac{x^2}{b^2} = 1
双曲线	\displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1	- a ：实半轴长度 - b ：虚半轴长度 - c ：焦点到中心的距离	c^2 = a^2 + b^2	焦点在实轴上（x轴方向） 若焦点在 y 轴，则标准形式为\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1
抛物线	y^2 = 2px 或 x^2 = 2py	- 不涉及 a, b, c 这样的统一参数	——	抛物线一般不使用 a, b, c 表示，而是用焦距 p

补充说明：

• 椭圆的离心率： e = \frac{c}{a} ，其中 0 < e < 1
• 双曲线的离心率： e = \frac{c}{a} ，其中 e > 1
• 圆是特殊的椭圆，满足 a = b ，此时 c = 0

几何特征与推论

曲线类型	几何特征/推论	说明
椭圆	离心率 e = \frac{c}{a} < 1	描述椭圆的扁平程度， c = \sqrt{a^2 - b^2}
	长轴、短轴	长轴为 2a ，短轴为 2b ，中心在原点或对称中心
	焦点	焦点在长轴上，距离中心为 c
	通径	椭圆通径长度为 \frac{2b^2}{a}
	对称性	关于 x 轴、y 轴及原点对称
	准线	两条准线方程为 x = \pm \frac{a}{e} 或 y = \pm \frac{a}{e}

曲线类型	几何特征/推论	说明
双曲线	离心率 e = \frac{c}{a} > 1	表示双曲线张开的程度， c = \sqrt{a^2 + b^2}
	实轴、虚轴	实轴长度为 2a ，虚轴长度为 2b
	渐近线	双曲线的渐近线方程为 y = \pm \frac{b}{a}x 或 x = \pm \frac{b}{a}y
	焦点	在实轴上，距离中心为 c
	通径	双曲线通径长度为 \frac{2b^2}{a}
	对称性	关于 x 轴、y 轴及原点对称
	准线	准线方程为 x = \pm \frac{a}{e} 或 y = \pm \frac{a}{e}

曲线类型	几何特征/推论	说明
抛物线	开口方向	由标准方程 y^2 = 2px 或 x^2 = 2py 决定
	焦点	如 y^2 = 2px 的焦点为 (p, 0)
	准线	如 y^2 = 2px 的准线为 x = -p
	通径	抛物线通径长度为 2p